スキルの効果に着目したチャンピオンのベクトル表現と類似度
Contents
はじめに
チャンピオンのベクトルでの表現について検討しました。
ベクトルを求めることによって、類似度を求められるため、それについても触れています。
そもそもなんでチャンピオンをベクトルとして数値で表し、その類似度を求めたかったかというと、類似度を使って以下のようなことができると考えたからです。
- チャンピオンの傾向を掴める
- プロシーンでのバン・ピックが理解しやすくなる
まずは、1. について。
具体的には、自分の得意チャンピオンや相手にして苦手なチャンピオンの傾向がわかるということがあります。
たとえば、アサシンが得意な方に対しては、ADCをする際にもアサシンと似たチャンピオンが得意であることが考えられます。
近接チャンピオンしか使ったことがなく、遠隔チャンピオンを試してみたいという方に似た特徴をもつチャンピオンをすすめることができれば、役に立ちそうであると考えられます。
また、苦手なチャンピオンについては、特定のチャンピオンを対策するのではなく、「苦手なチャンピオンのような、急に距離を詰めてくるチャンピオンたち」というくくりができれば、対策もしやすいはずです。
次に、2. について。
プロシーンのでのバン・ピックには、パッチのバージョンやチーム毎に傾向があるように思います。
たとえば、ボットレーンには、ブリンクスキルを持つチャンピオン(
、
)を取ることやジャングラーにはCCを複数持つチャンピオン(
、
)を取ることが多いなど。
このような、ブリンクスキルを持つことや、CCを複数持つということを数値で表すことができれば、なんでこのチャンピオンがピックされたのかということが理解しやすくなるように思います。
また、数値で表せることによって、検討できることも増えます。
先ほどの例を用いると、CCを複数持つチャンピオンであるセジュアニやスカーナーはプロシーンでピックされるのに、なんで
アムムはピックされないのか？などが検討可能になります。
CCを複数持つという条件は一致しているけど、「何か」が違うからピックされず、その「何か」がわかれば、さらに楽しめそうですね。
ただ、今回の検討だけでは、2. について大部分を説明することは難しいです。
将来的にできるようにするための、1つの検討といった位置づけになります。
まだいくつか検討項目が残っており、それが完了すれば、傾向は説明できるような気がしているので、いい結果が出ればその際に。
1. については、今回の記事でそれらしい結果が出ていますので、最後まで目を通していただければと思います。
ベクトル
ベクトルと聞くと矢印の印象が強いですが、ここでは少し違った意味を示します。
wikipediaでのベクトルの説明 のコンピュータの項目に書かれている1次元の配列として表現されるデータ構造を意味します。
ベクトルの定義については、こちら のページがわかりやすかったので、
その説明をお借りすると、
実\(n\)次元数ベクトル は、実数を\(n\)個並べたもの
すなわち、
実数体\(R\)から実数\(v_1, v_2, …, v_n\)をとって順序をつけた、\(n\)組
\(v= ( v_1, v_2, …, v_n )\) ただし、\(v_1∈R\)かつ\(v_2∈R\)かつ…かつ\(v_n∈R\)
のことを、
実\(n\)次元数ベクトル、\(n\)次元実ベクトル、\(n\)項実ベクトルなどという。上記の\(v_1\)をベクトル\(v\)の第1成分、
上記の\(v_2\)をベクトル\(v\)の第2成分、
：
上記の\(v_n\)をベクトル\(v\)の第n成分
と呼ぶ。参考元: 数学についてのwebノート
と 書かれています。
要は、ベクトルとは、数字を並べたものと考えてください。
具体例を用いて説明します。
上記では、動物をベクトルで表しています。
第1成分から体重、首の長さ、鼻の長さ、足の数、背びれの数値を表しています。
ベクトルがどの動物と対応しているかわかっていなくても、第2成分が首の長さを表していることを知っていると、\(b\)は他と比べて大きいことを考えると、キリンを表していそう？と考えることができます。
このようにベクトルはその動物の特徴を表しているといえるので、特徴ベクトルといったりもします。ここでは単にベクトルといいます。
また、ベクトルには、和とスカラー(定数倍)が定義されています。
たとえば、キリンとゾウの1頭ずつの体重を求めようとした場合には、\(a\)と\(b\)を足して、第1成分をみれば6800kgが得られます。
そして、そのときの足の本数も第4成分をみると8本ということが得られます。
また、イルカ3頭の場合を考えても、\(c\)を3倍して、第1成分を見れば合計体重が得られます。
これも同様に、そのときの背びれの数が3枚だということも第5成分をみることでわかります。
このようにベクトルを使うことによって、実数をまとめて扱いやすくなります。
また、コサイン類似度使うことによって、ベクトル同士の類似度を求めることができます。
コサイン類似度の定義は以下のとおり。
\(a= ( a_1, a_2, \cdots , a_n )\) と \(b= ( b_1, b_2, \cdots , b_n )\)に対して
\( \Large{ \frac{a_1b_1+ \cdots + a_nb_n}{ \sqrt{a^2_1+\cdots+a^2_n} \sqrt{b^2_1+\cdots+b^2_n} } }\)
をコサイン類似度という
参考元: 高校数学の美しい物語
このようにベクトルで表現することで、数値を扱いやすくなり、その類似度も求められるため、ベクトルについて検討することは重要となってきます。
以降でチャンピオンをベクトルで表現する方法について説明します。
チャンピオンのベクトル表現
チャンピオンの特徴
前節では、動物の特徴をベクトルで表現する方法について述べました。
ここでは、チャンピオンの特徴をどのようにベクトルで表現するかを考えます。
チャンピオンはそれぞれ基礎ステータスとスキルを持っています。
本記事では、スキルにのみ着目してチャンピオンの特徴をベクトルで表現します。
理由は以下の2つ。
- 基礎ステータスを考慮すると、役割が偏ってしまう
- 既に数値で表されているため、スキルより検討することが少ない
まず1. については、役割が偏ってしまうことを懸念しているためです。
たとえば、基礎ステータスには、射程も含まれており、これが類似度に用いられると、遠隔チャンピオンの中で類似度が高くなってしまいます。
はじめにでも言いましたが、近接チャンピオンだけでなく、遠隔チャンピオンに挑戦したいのに、遠隔チャンピオンばかりで固まってしまうと、視野が狭まってしまいます。
広い視野を得るために、まずはスキルだけでの類似度を検討しておく必要だと考えました。
必要な場面では基礎ステータスも考慮する必要がありますが、ここでの議論では用いません。
次に、2. について。
基礎ステータスは既に数値となっているため、一次元配列で表現することは容易です。
一方で、ブリンクをもっている、CCを複数持つということに関しては、数値にするための検討が必要だと考えました。
以上のことから、チャンピオンの特徴をスキルに着目してベクトルでの表現について考えていきます。
チャンピオンの表現方法
実際にチャンピオンのスキルについて見ていきます。
具体例として、
アニビアを使って説明します。
まずは、スキルの説明を見てみます。
Q: 指定方向に両翼で力強く羽ばたいて、氷の塊を放つ。氷は触れた敵に魔法ダメージと「チルド」を与える。最大距離に達するかこのスキルを再使用すると氷の塊が炸裂して、範囲内の敵にダメージとスタンを与える。
W: 空気中の水分を凝縮して氷の壁をつくり、相手の移動を妨害する。壁は数秒後に溶けて消滅する。
E: 翼をはためかせて対象を凍てつく氷柱で攻撃し、小ダメージを与える。直前に「フラッシュフロスト」でスタンされているか、最大範囲の「ブリザード」でダメージを受けた対象には、2倍のダメージを与える。
R: 指定範囲に激しい吹雪を召喚する。吹雪は範囲内の敵に継続ダメージを与え「チルド」を付与する。
P: 体力がゼロになると卵状態になる。卵の状態で6秒経過すると復活する。
説明には、チャンピオンとスキルの見た目に関する説明(例: 羽ばたいて、氷の塊、吹雪)とゲーム内の状況を変化させる説明(例: 敵にダメージ、スタンを与える、相手の移動を妨害する)が見受けられます。
本記事では、ゲーム内での効果を類似度として求めたいため、ゲーム内の状況を変化させる効果のみ着目します。
アニビアをゲーム内の状況を変化させる説明のみで表現すると、以下の効果を持つチャンピオンであるという説明ができそうです。
- 指定方向のスキルを持つ
- 相手にマーク(チルド)を付ける
- 相手をスタンさせる
- 行動を妨害する壁を作る
- 指定範囲のスキルを持つ
- 継続ダメージを与える
- 復活スキルを持つ
また、これらの効果は他のチャンピオンにも含まれているものもあります。
たとえば、スタンは
アリスターや
ナーも持っています。
アリスターは、アニビアの持っていない味方を回復させるという効果をもち、それは
ナミも持っていたりします。
つまり、スキルの効果は複数のチャンピオンに保有されているという関係があります。
図で表すと以下のとおり。
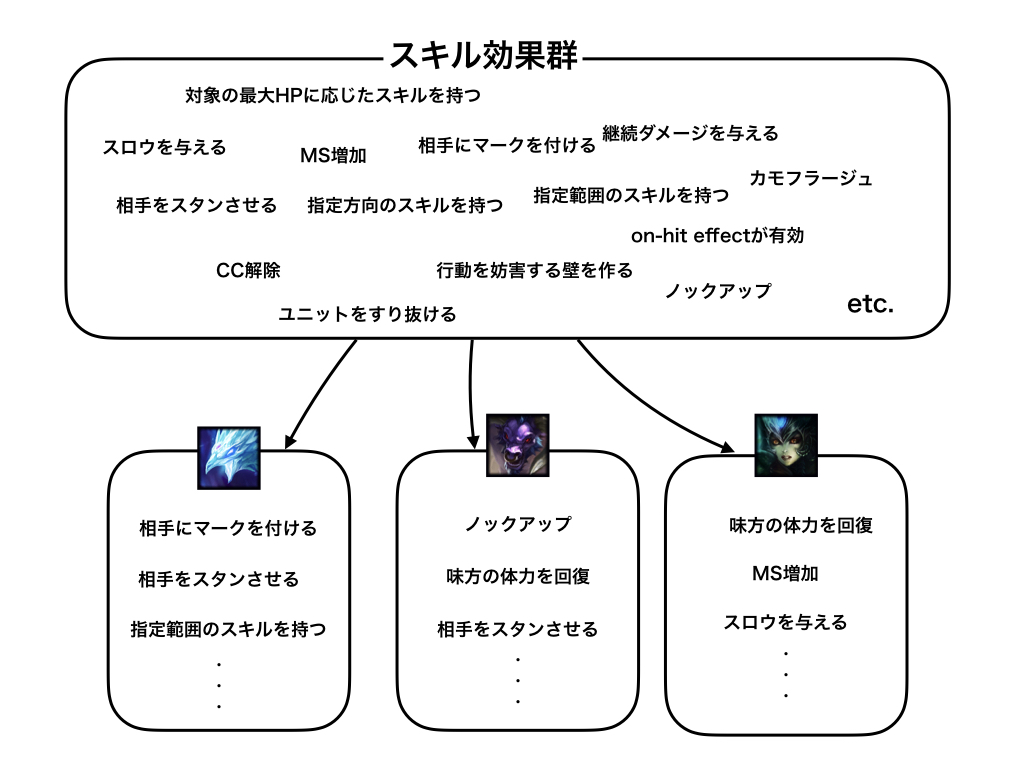
スキル効果群というものから、いくつか選択して、それ集合として考えると、チャンピオンの特徴を説明できると考えられます。
また、その集合には、要素が重複するものも存在する(例: 指定方向スキルを2つ持つ場合など)。
以上のことから、チャンピオンの特徴は、スキルの効果の多重集合(multiset, bag)であると考えられます。
このような多重集合を用いてある物事を説明している方法に、 Bag of Wordsというものがあります。
Bag of Wordsは文や文書を単語の出現頻度の多重集合で表す方法で、自然言語処理や情報検索の分野で用いられています。
文法や単語の順序さえ無視しますが、多重度は維持しています
単語の出現頻度は、文書の特徴を表しており、類似度を求めることに使われています。
たとえば、appleという単語を頻繁に使っている文書同士は似ているとといったように。
このようなBag of 〇〇 という考え方は、文書の分類以外でも使われています。
具体的には、画像の表現(Bag of Features)や顧客の購入履歴(Bag of Items)といったものがあります。
そこで、チャンピオンがスキルの効果の多重集合として考えられるのであれば、Bag of Wordsの表現方法にしたがって、ベクトルで表現できれば、類似度を求められるのではないかと考えました。
以降ではBag of Wordsについて説明し、その考え方をチャンピオンに用いる方法について述べていきます。
Bag of Words
Bag of Wordsは単語の出現回数をベクトルとして表現します。
例として、以下の2つの文書があったとします。
- John likes to watch movies. Mary too likes movies.
- Mary also likes to watch football games.
これらの文書には John, likes, to, watch, movies, Mary, too, also, football, gamesの10語が用いられており、ベクトルで表すと以下のようになります。
- (1, 2, 1, 1, 2, 1, 1, 0, 0, 0)
- (0, 1, 1, 1, 0, 1, 0, 1, 1, 1)
第1成分は、Johnの出現回数に対応しており、第2成分は、likesの出現回数と対応しています。
これをすべての成分を対応させると上記のような表現ができるわけですね。
また、1. のベクトルは(1, 0, 0, 0, 0, 0, 0, 0, 0, 0)を1個、(0, 1, 0, 0, 0, 0, 0, 0, 0, 0)を2個、…、(0, 0, 0, 0, 0, 0, 0, 0, 0, 1)を0個といったように、各成分が1で残りの成分がすべて0であるベクトルを足したベクトルという表現もできます。
このような各成分が1で残りの成分がすべて0であるベクトルをone-hotベクトルと呼びます。
なので、Bag of Wordsにおける単語の表現は(1, 0, 0, 0, 0, 0, 0, 0, 0, 0)のようなone-hotベクトルになります。
チャンピオンにおけるBag of Words
本節では、Bag of Wordsの考え方を使って、実際にチャンピオンをベクトルで表現していきます。
しかし、表現しようとしたとき、one-hotベクトルをどのように定義すべきかという問題があります。
文書の場合だと、すべての文書に登場する単語を取得し、それに順序を付けることでone-hotベクトルは得られます。
しかし、チャンピオンの場合には、すべてのスキル効果について考える必要があります。
例では、スキルの説明からわかりそうな、「継続ダメージ」や「スタンを与える」という要素がありそうだと書きましたが、これがどの粒度でいくつあるのかという部分を明確にしなければなりません。
チャンピオンのスキル説明を単語に分け、それをone-hotベクトルとする考え方もありますが、スキルの説明には、氷や炎といったゲーム内とは関係のない用語が使われていたり、体力を回復するのは、自分だけか味方だけかなど、複雑な構造をしています。
スタンという単語だけ拾ったとすると、アニビアのEは「スタンしている相手に」という説明が含まれており、スタン要素をもっている？と判断されかねません。
これらのことから、説明をそのまま用いることは、難しそうです。
また、壁には、ノックバック判定があり、
トランドルの
Eと同じ効果があるのですが、説明だけだとその意味を汲み取れません。
これを解決するためには、一度プレイし、人間の理解に基づき、まとめる作業が必要になります。
この作業をいちから実施してもよいのですが、多くの工数が必要であることと作業者の理解に偏りが発生する可能性があります。
確認すればある程度統一できそうですが、確認の工数も考慮すると実現が難しくなってきます。
なので、人間の理解に基づき、複数人の監視のもとでスキルについてまとめられている既存の情報を用いることが望ましい。
この条件を満たすのが、League of Lengeds wiki の情報です。
このサイトには、チャンピオン毎のページが存在し、スキルの説明も含まれます。
▼チャンピオンページのスキル説明例
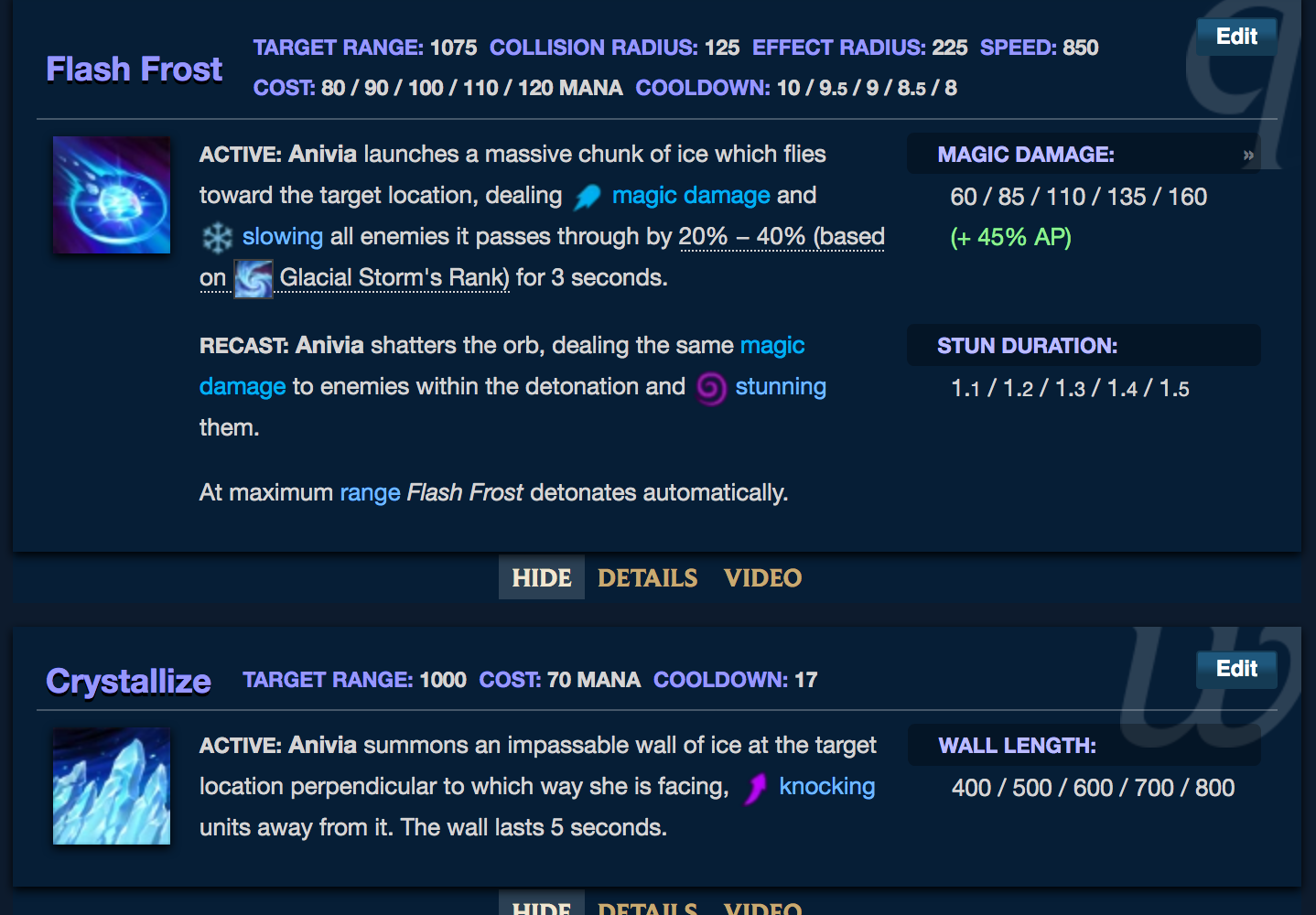
スキルの説明には、要素のリンクが張られており、その先には、他に同じ効果を持つチャンピオンを確認できます。
▼同じ効果を持つチャンピオン例
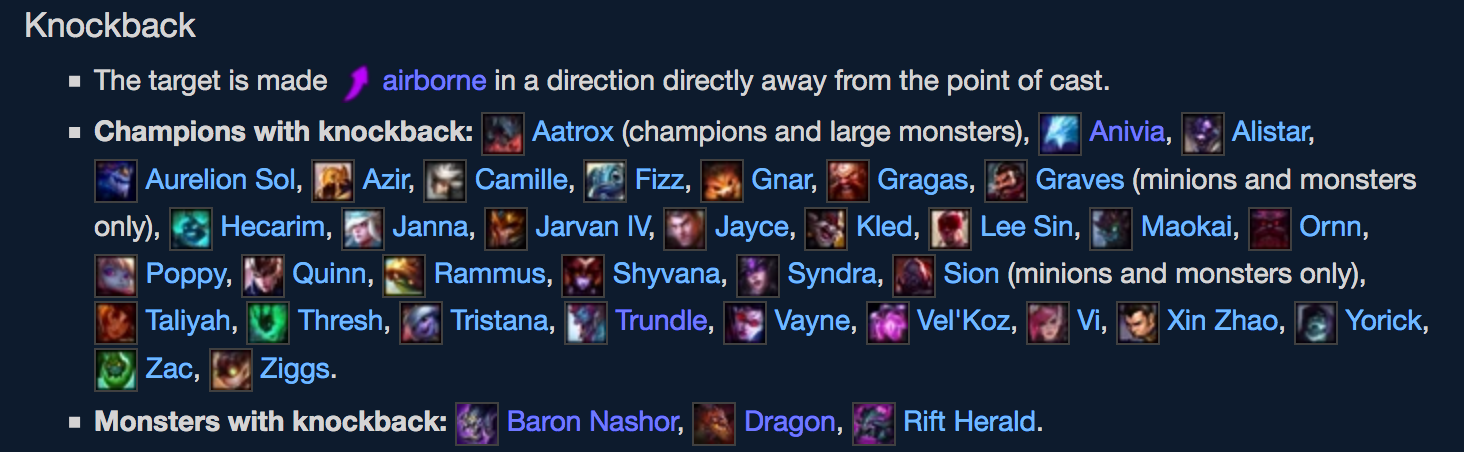
このため、wikiで説明されている単位で説明すると、スキルの効果について説明できそうであるということがわかります。
以降でwikiでの取得方法について説明します。
Wikiからの情報取得
前節では、wikiのリンクが存在する単位でスキルの説明ができそうであることを述べました。
実際に、リンク先には、Healingの項目に自分自身だけや味方も含むという単位でわかれています。
なので、粒度としては、チャンピオンのスキルの説明内に存在するリンク先の段落毎に分けるのが良いと考えました。
▼スキルの説明ページで段落が分かれている例
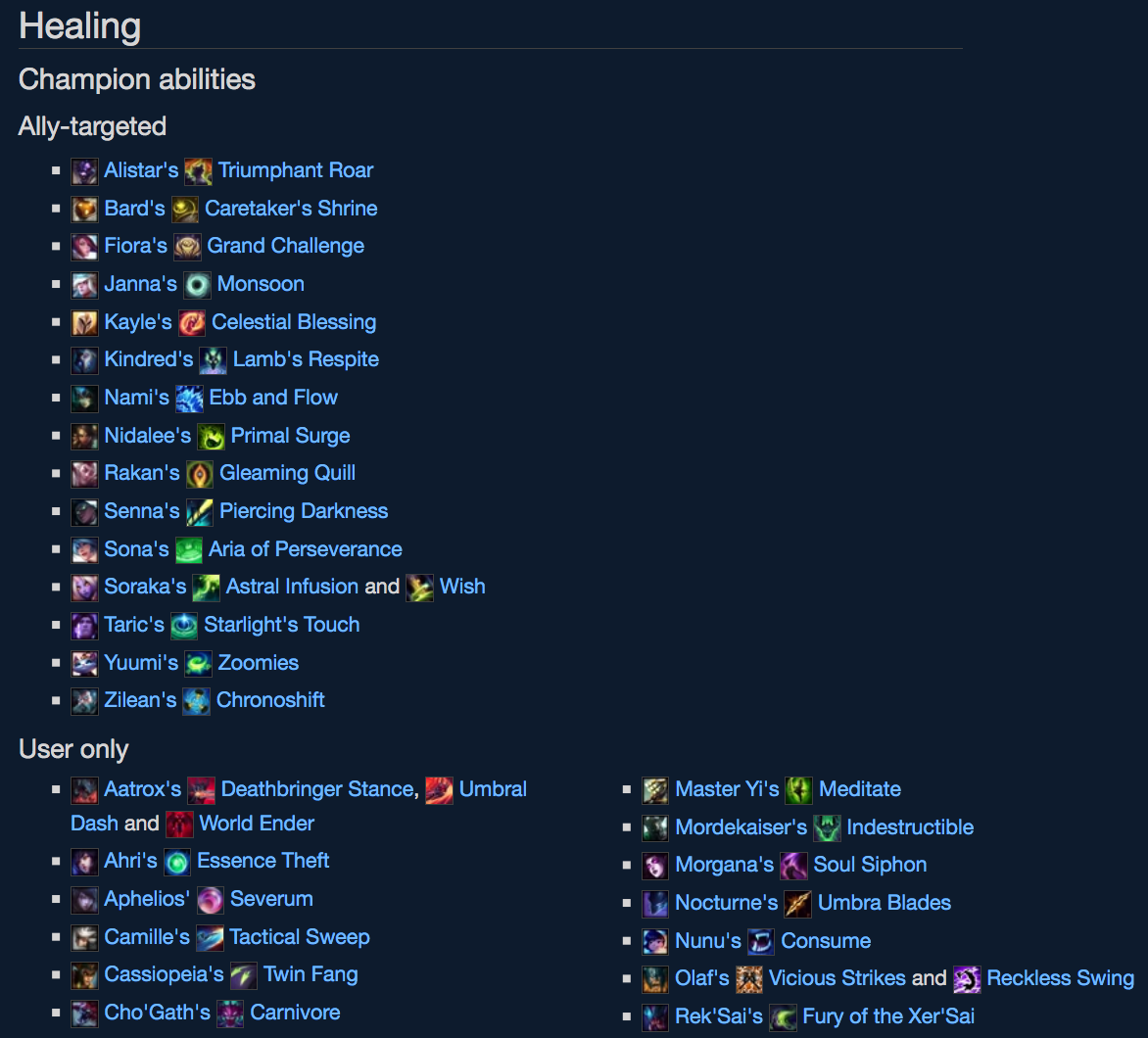
上の例では、同じHealingのページに存在しますが、Ally-targetd と Userd only は別のスキル効果として扱っています。
この方法で要素を取得すると、チャンピオンのスキル説明内に使用されているリンクの数は 84個、リンク先に存在するすべての段落の数は 223個となりました。
つまり、チャンピオンは223個の成分によって表せそうだということがわかります。
パッチのバージョンは10.4のときのものを使用しています。
また、
Rhaastと
ShadowAssassinはWiki上で別チャンピオンとして数えられているため、これらもベクトルで表現しています。
なので、148チャンピオン + 2(Rhaast, ShadowAssassin)、計150個のベクトルを生成しました。
ただし、あくまでもスキルの効果の集合で表しているだけであって、プレイスタイルまで表現できているわけではありません。
射程や攻撃力といった基礎ステータスやクールダウン、ダメージの量などは考慮していないため、レイトゲームキャリーであることや殴り合いが強いといったことは表現できていないことに注意してください。
tf-idfによる重要度の評価
前節で得られたベクトルにの重要度の評価を行います。
出現頻度だけ数えてそれをそのまま使ってしまうと、多くの文書やチャンピオンに登場する成分が類似度に大きく影響を与えてしまいます。
たとえば、文書の場合では、「a」、「the」、「to」などがあり、チャンピオンでは、「方向指定のスキルである」といった成分が該当します。
このような成分より、ある特定の文書、チャンピオンにしか登場していない成分を評価するほうがよいと考えられます。
チャンピオンの場合で考えると、「チャーム」や「サプレッション」は、特定のチャンピオンしか持っておらず、そのチャンピオンの特徴を他の要素と比べて大きく表していると考えられます。
このようなことに、tf-idfによる重要度の評価で対処します。
文書中に含まれる単語の重要度を評価する手法の1つです。
tf-idfは、tf（Term Frequency、単語の出現頻度）とidf（Inverse Document Frequency、逆文書頻度）の二つの指標に基づいて計算されます。
計算式は以下のとおり。
$$tfidf_{i,j}=tf_{i,j} \cdot idf_{i,j}$$
$$tf_{i,j}=\frac{文書d_jに登場する単語t_iの数}{文書d_jに登場する全ての単語の数}$$
$$idf_{i,j}=\log{\frac{総文書数}{単語t_iが含まれる文書の数}}$$
idfでは、単語が含まれる文書の数を分母に取ることから、多くの文書に出現する語は重要度が下がり、特定の文書にしか出現しない単語の重要度を上げることができます。
ベクトル表現の課題
これまでの説明により、チャンピオンをベクトルで表現でき、重要度も評価したため、特徴をベクトルで表せたといえます。
しかし、これを使って、チャンピオンの類似度を求めると、限られた成分での類似度しか求められず、実際に似ていると判断することは難しいです。
以下に2つのベクトルの類似度を求める例を示しています。
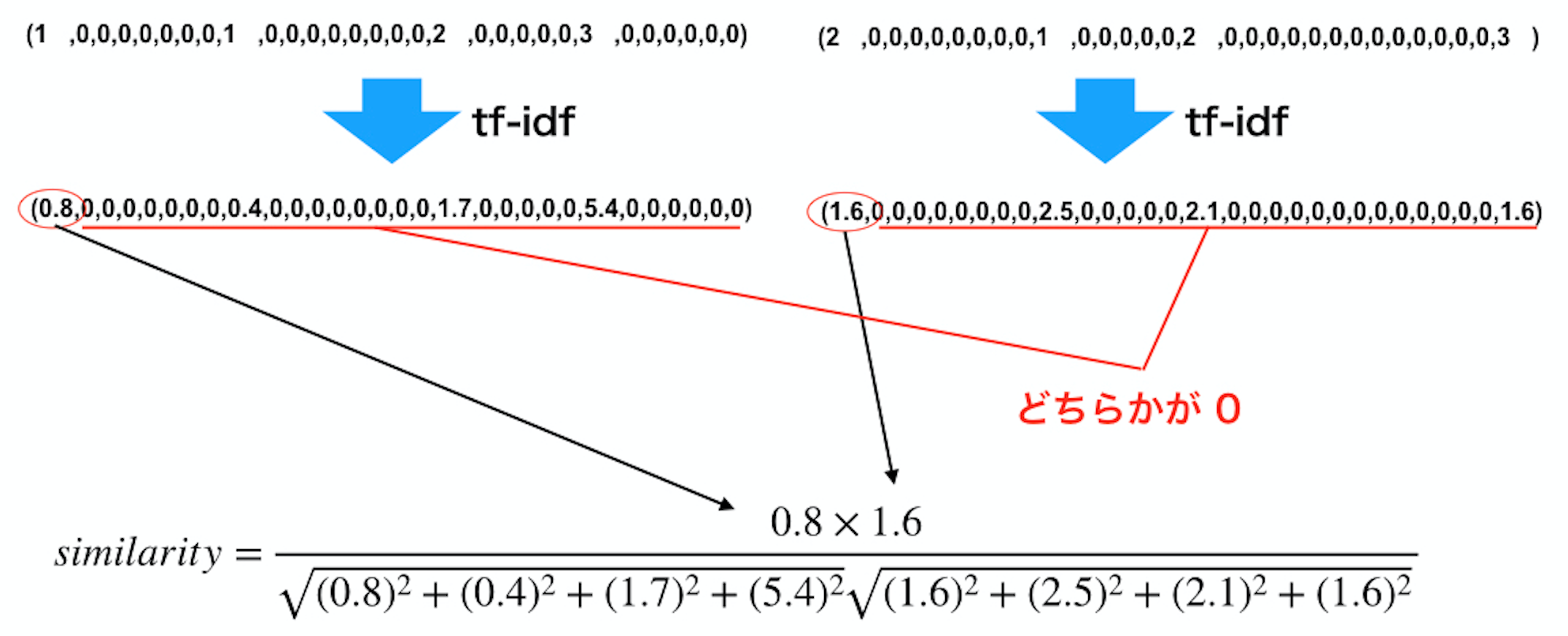
お互いの成分には持っているスキルの効果の数を表しています。
実際に類似度を求めると、ほとんど要素が0であり、共通して持っている特徴の第1成分しか考慮されません。
具体的にいうと、スタンとノックアップのように、相手の移動を制限する点で似ているのにも関わらず、別成分で表現しているため、類似度は高くならず、希少なスキルを持っていればそれだけで類似度が高くなってしまいます。
このようになってしまう原因としてチャンピオンを表現するベクトルがまばら(ほとんど要素が0)であるということがあります。
実際に得られた数値を見てみると、ベクトル毎の0でない成分の数の平均は17、と少ないことがわかります。
0の成分が多く、1つの成分に集まっているかというとそういうわけでもなく、1つのベクトルに含まれるスキルの効果の数の平均は20、 とこちらも少ない。
これはゲームバランスを考えると、十分に納得できます。
味方を強化できて、ブリンク、移動速度上昇を持ち、CCを数種類持ち、復活して、ステルスを持つチャンピオンはいませんね。
また、移動速度上昇のようなステータスを上昇させる効果は、固定値か割合で上昇するかといったところまで分かれています。
このため、同じステータスを上昇させるスキルでも、固定値か割合かが違うだけで別スキルとして扱われます。
このように各成分には、1つにまとめられそうな関係のものもあり、いくつかまとめて考えると、直感的に扱いやすい類似度が求められそうな気がします。
ただし、このまとめる作業を人間の判断で行うのは困難です。
たとえば、ハードCCやソフトCCという成分にまとめることを考えると、アリスターの
Qと
ブリッツの
Qを同じ扱いにすることになってしまうので、それを良しとするかの判断が必要です。
また、ハードCCとソフトCCのような概念が存在するものであれば考えやすいのですが、一緒にしてよいか否かの判断が難しいものもあります。
具体的には、魔法防御貫通の固定値と割合をどう扱うかというものがあります。
これは、
モレロノミコンを買うか
ヴォイドスタッフを買うかという議論も存在しますし、これを魔法防御貫通という一括りにするという判断も難しいです。
このように、ベクトルがまばらであるため、類似度を求めづらく、かつ人間の判断で成分をまとめることも難しい、という課題が存在します。
ここで重要となってくるのが、スキルの効果同士に多少の類似度が存在しそうだ、と考えられることです。
つまり、スキルの効果同士の類似度を考慮できれば、課題に対処できそうだと考えられます。
そこで、スキルの効果同士の類似度を表す行列を得るために、潜在意味解析を使います。
潜在意味解析
潜在意味解析とは
潜在意味解析とは、自然言語処理の手法の1つで、文書群とそこに含まれる単語群について、それらに関連した概念の集合を生成することで、その関係を分析する技術のことを指します。
関連した概念の集合をトピックと呼びます。
たとえば、以下の3つの単語の集合をみてみると、
- baseball, tennis, ball, field, play, hit
- watch, film, play, streaming, media, pause
- song, play, dance, song, rhythm,band
上から、スポーツ、動画、音楽について表している集合だと考えることができます。
それを意味する単語が集合に含まれていないのにも関わらず、この3つの単語を想起できると思います。
これは、複数の単語の共起性から得られる情報により、想起できたと考えることができ、このような情報を「潜在意味」と呼びます。
また、これらは関連した概念であると考えると、スポーツトピック、動画トピック、音楽トピックと考えることもできます。
このように単語間には何かしらの関連があり、ある概念によってまとめることができます。
まとめることができれば、スポーツトピックに含まれる単語が出現したもの同士で類似度を示すことができます。
これを利用することにより、スキルのトピックを作成することができれば、前述した課題を解決できそうだと考えられます。
以降では、潜在意味解析の1つである潜在意味索引(Latent Semantic Indexing, LSI)を用いて、実際にトピックを取得します。
潜在意味索引
LSIでは、特異値分解(singular value decomposition, SVD) と呼ばれる行列分解を用いて定式化した後に、特異値の大きい順にランクを削減することにより、新たな行列を得ます。
ここで行列とは、列ベクトルを横に、あるいは行ベクトルを縦にいくつか並べたものを指します。
特異値分解の流れは以下のとおり。
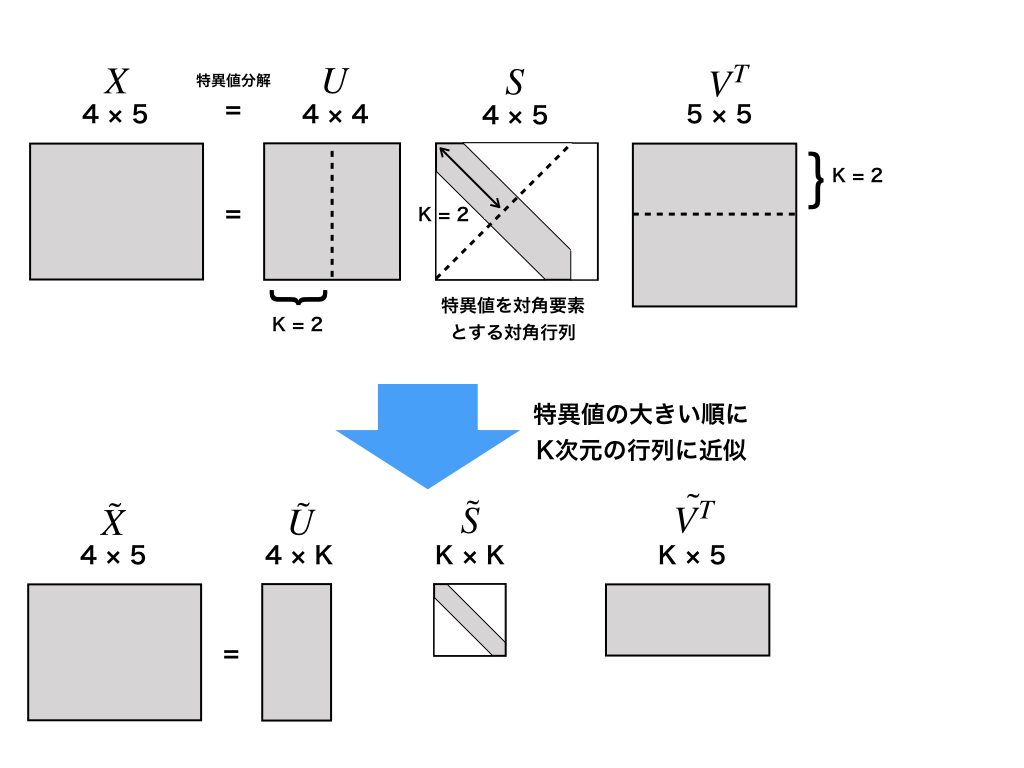
行列\(X\)を、 \(X=USV^T\) を満たすような行列\(U, S, V\)へと分解します。
\(S\)は対角行列で、対角要素を特異値と呼ぶ。\(U, S, V\)の各列ベクトルを特異値が大きい順にK個用いて、新たに\(\tilde{U}, \tilde{S}, \tilde{V}\) を作成し、 \(\tilde{X} = \tilde{U}\tilde{S}\tilde{V}^T\)とすることで、\(\tilde{X}\)を得ます。
これは、低ランク近似と呼ばれる行列の近似で、ランクK の\(X\)への近似を最小誤差で得ることができているそうです。
具体例は以下のとおり。(参考: トピックモデルによる統計的潜在意味解析 図1.4 より)
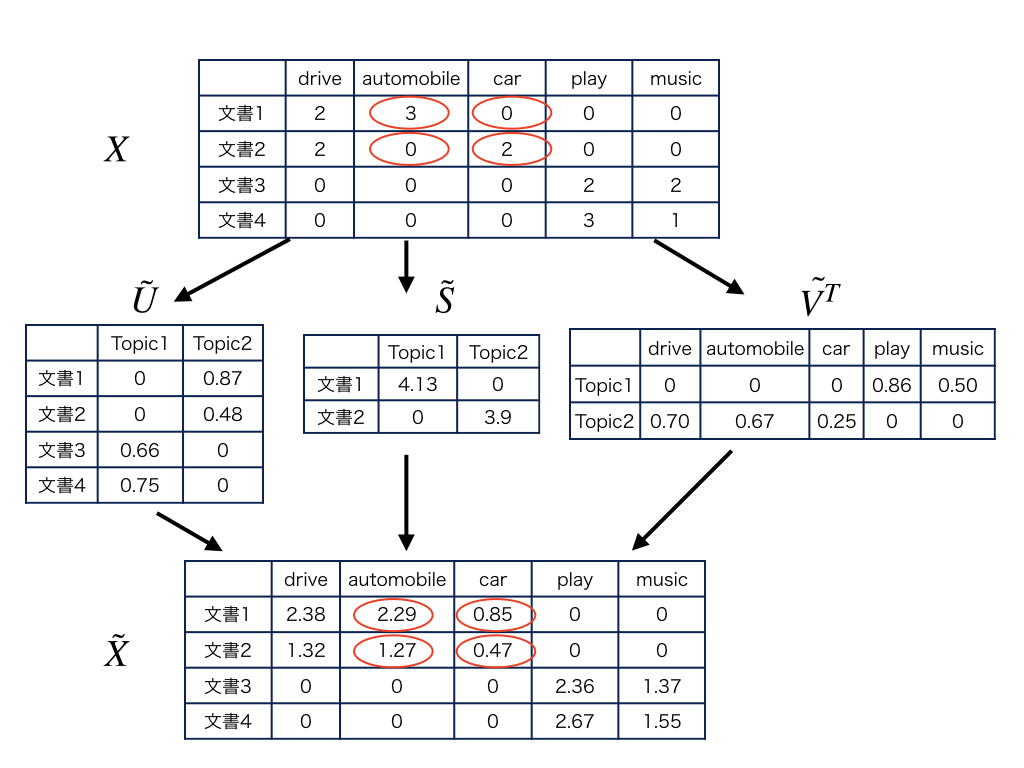
行列\(X\)では、文書1に「car」の出現回数は0となっており、文書2では、「automobile」の出現回数が0となっています。
一方で、行列\(\tilde{X}\)では、文書1、文書2ともに「car」や「automobile」の出現回数が0でないことがわかります。
これは、「drive」という単語との共起性から「car」や「automobile」の潜在的意味が抽出されていると考えられます。
また、各特異ベクトルは潜在的意味に関する情報を表しています。
たとえば、\(\tilde{V}\)の第二列ベクトルは、「drive」,「automobile」,「car」の要素に値があり、その他の単語が0であることから、これらの単語の共起性に関する情報であることがわかります。
ここで重要なのは、「automobile」と「car」は、文書中で共起していないにも関わらず、このような共起性を抽出できる点です。
\(\tilde{V}\)の\(k\)番目の各要素が表しているのは、潜在トピック\(k\)と各単語の共起度であり、その数値をみることによって潜在トピック\(k\)が創発する意味を解釈できます。
次に、\(\tilde{U}\)についてみてみると、\(\tilde{U}\)の第一列ベクトルは 文書3と文書4の要素に値があり、文書1と文書2の要素の値が0であることがわかります。
これは、トピック1と、文書3と文書4の共起性を表していると考えられます。
また、\(\tilde{U}\)の行列ベクトルは、各文書におけるトピックの共起度とみることができます。
つまり、文書1では、トピック1が0.87回現れているというようにみることができます。
このようにSVDを行い、ランクを削減して、新たな行列を用いることがLSIの考え方になります。
U,S,Vの求め方
実際に特異値分解を行い、低ランク近似行列を得るために、U,S,Vの求め方について触れておきます。
まず、MxNの行列\(X\)を\(U,S,V^T\) に分解することを目的としているため、\(X=USV^T\)と置き、\(XX^T\)を求めると、
$$
\begin{eqnarray}
XX^T&=&USV^T(USV^T)^T \\
&=&USV^TVS^TU^T \\
&=&USS^TU^T \\
&=&US^2_MU^T \\
\end{eqnarray}
$$
となります。
少し補足すると、1段目は、\((AB)^T=B^TA^T\)を使い、2段目は、\(V\)が直行行列であるため、 \(V^TV=VV^T=E\)を使っています。
3段目以降は、\(S\)が対角行列であるから以下のようになります。
$$
S = \left(
\begin{array}{ccc}
\lambda_1 & \cdots & 0 \\
\vdots & \ddots & \vdots \\
0 & \cdots & \lambda_l
\end{array}
\right)
$$
ただ、\(S\)はMxN行列であるため、正方行列ではありません。
M>Nならば、0を埋めて縦に長くになり、このとき\(l\)=Nになる。
M<Nならば、0を埋めて横に長くなり、このとき\(l\)=Mになる。
\(SS^T\)は、MxN行列とNxM行列の積になるため、MxM行列が得られる。
\(S^2_M\)は、以下のようになります。
$$
S^2_M = \left(
\begin{array}{ccccc}
\lambda^2_1 & \cdots & 0 && \\
\vdots & \ddots & \vdots && \\
0 & \cdots & \lambda^2_l && \\
&&& 0 & \\
&&&& 0 \\
\end{array}
\right)
$$
ここまでが式展開の補足になります。
先ほど得られた式に、右から\(U\)をかけると、
$$XX^TU=US^2_M$$
となります。
行列\(U\)はベクトル\(u\)を並べたものと考えると、\(U\)の\(i\)番目が\(S^2\)の\(i\)番目と掛け合わせたものであると考えることができるため、
$$XX^Tu_i=\lambda^2_iu_i$$
と書くことができます。(\(\lambda^2_i\)は定数であるため、先に書いても問題ない。)
ここで、固有値と固有ベクトルの定義をみてみます。
正方行列\(A\)，0でないベクトル\(x\)，スカラー \(\lambda\) の間に
\(\Large{Ax=\lambda x}\)
が成立するとき\(x\)を\(A\)の固有ベクトル，\(\lambda\)を\(A\)の固有値と言う。参考元: 高校数学の美しい物語
定義と先ほど得られた式から、\(XX^T\)の固有値\(\lambda^2_i\)と固有ベクトル\(u_i\)を求めることでこれらを得られます。
固有値と固有ベクトルの求め方は参考元にわかりやすく記載されていますので、そちらを参照してください。
これにより、\(U, S\)を求めることができます。
同様に、\(X^TX\)から\(V, S\)を得られるため、\(XX^T\)と\(X^TX\)から\(U, S, V\)を求められます。
結果
類似度
tfidfで得られたベクトルを正規化(長さと1に)したものとLSIによって得られた結果を示します。
LSIの対象の行列は、tfidfで得られた行列を正規化したベクトルを並べたものを対象としています。
なお、LSIの近似する行列のランクは 20(1チャンピオンが持っているスキルの効果の平均)としています。
トピックの数は、今後詳しく検討する必要があると思っていますが、それは追々。
得られた結果は以下のとおり。(横スクロールで全チャンピオン見れます)
▼tfidfで得られたベクトルの類似度
| Ranking |  Aatrox |
 Ahri |
 Akali |
Alistar |
Amumu |
Anivia |
 Annie |
 Aphelios |
 Ashe |
 AurelionSol |
 Azir |
 Bard |
Blitzcrank |
 Brand |
 Braum |
 Caitlyn |
 Camille |
 Cassiopeia |
 Chogath |
 Corki |
 Darius |
 Diana |
 Draven |
 DrMundo |
 Ekko |
 Elise |
 Evelynn |
Ezreal |
 Fiddlesticks |
 Fiora |
 Fizz |
 Galio |
 Gangplank |
 Garen |
Gnar |
 Gragas |
 Graves |
 Hecarim |
 Heimerdinger |
 Illaoi |
 Irelia |
 Ivern |
 Janna |
 JarvanIV |
 Jax |
 Jayce |
 Jhin |
 Jinx |
 Kaisa |
 Kalista |
 Karma |
 Karthus |
 Kassadin |
 Katarina |
 Kayle |
 Kayn |
 Kennen |
 Khazix |
 Kindred |
 Kled |
 KogMaw |
 Leblanc |
 LeeSin |
 Leona |
 Lissandra |
Lucian |
 Lulu |
 Lux |
 Malphite |
 Malzahar |
 Maokai |
 MasterYi |
 MissFortune |
 MonkeyKing |
 Mordekaiser |
 Morgana |
Nami |
 Nasus |
 Nautilus |
 Neeko |
 Nidalee |
 Nocturne |
 Nunu |
 Olaf |
 Orianna |
 Ornn |
 Pantheon |
 Poppy |
 Pyke |
 Qiyana |
 Quinn |
 Rakan |
 Rammus |
 RekSai |
 Renekton |
 Rengar |
 Riven |
 Rumble |
 Ryze |
Sejuani |
 Senna |
 Sett |
 Shaco |
 Shen |
 Shyvana |
 Singed |
 Sion |
 Sivir |
Skarner |
 Sona |
 Soraka |
 Swain |
 Sylas |
 Syndra |
 TahmKench |
 Taliyah |
 Talon |
 Taric |
 Teemo |
 Thresh |
 Tristana |
Trundle |
 Tryndamere |
 TwistedFate |
 Twitch |
 Udyr |
 Urgot |
 Varus |
 Vayne |
 Veigar |
 Velkoz |
 Vi |
 Viktor |
 Vladimir |
 Volibear |
 Warwick |
 Xayah |
 Xerath |
 XinZhao |
 Yasuo |
 Yorick |
 Yuumi |
 Zac |
 Zed |
 Ziggs |
 Zilean |
 Zoe |
 Zyra |
Rhaast |
ShadowAssassin |
| 1 | (0.4) |
(0.42) |
(0.31) |
(0.26) |
(0.31) |
(0.38) |
(0.29) |
(0.35) |
(0.7) |
(0.37) |
(0.41) |
(0.37) |
(0.36) |
(0.62) |
(0.55) |
(0.4) |
(0.39) |
(0.62) |
(0.28) |
(0.42) |
(0.39) |
(0.39) |
(0.36) |
(0.53) |
(0.44) |
(0.44) |
(0.42) |
(0.37) |
(0.43) |
(0.56) |
(0.44) |
(0.26) |
(0.41) |
(0.32) |
(0.38) |
(0.39) |
(0.31) |
(0.36) |
(0.63) |
(0.48) |
(0.36) |
(0.33) |
(0.46) |
(0.31) |
(0.39) |
(0.41) |
(0.7) |
(0.43) |
(0.36) |
(0.26) |
(0.4) |
(0.61) |
(0.53) |
(0.39) |
(0.41) |
(0.32) |
(0.36) |
(0.39) |
(0.53) |
(0.35) |
(0.61) |
(0.41) |
(0.4) |
(0.55) |
(0.38) |
(0.31) |
(0.5) |
(0.39) |
(0.44) |
(0.43) |
(0.43) |
(0.39) |
(0.41) |
(0.48) |
(0.35) |
(0.36) |
(0.5) |
(0.39) |
(0.41) |
(0.42) |
(0.45) |
(0.36) |
(0.3) |
(0.49) |
(0.38) |
(0.34) |
(0.39) |
(0.4) |
(0.35) |
(0.32) |
(0.49) |
(0.46) |
(0.39) |
(0.32) |
(0.37) |
(0.3) |
(0.37) |
(0.24) |
(0.53) |
(0.4) |
(0.4) |
(0.37) |
(0.55) |
(0.28) |
(0.42) |
(0.51) |
(0.26) |
(0.37) |
(0.39) |
(0.43) |
(0.53) |
(0.45) |
(0.38) |
(0.41) |
(0.25) |
(0.35) |
(0.39) |
(0.44) |
(0.45) |
(0.36) |
(0.37) |
(0.42) |
(0.42) |
(0.36) |
(0.39) |
(0.21) |
(0.29) |
(0.42) |
(0.3) |
(0.37) |
(0.37) |
(0.39) |
(0.36) |
(0.46) |
(0.33) |
(0.41) |
(0.49) |
(0.42) |
(0.43) |
(0.42) |
(0.57) |
(0.41) |
(0.33) |
(0.38) |
(0.36) |
(0.38) |
(0.32) |
(0.63) |
(0.4) |
(0.28) |
| 2 | (0.39) |
(0.33) |
(0.3) |
(0.26) |
(0.31) |
(0.37) |
(0.26) |
(0.29) |
(0.56) |
(0.29) |
(0.28) |
(0.36) |
(0.32) |
(0.41) |
(0.47) |
(0.37) |
(0.27) |
(0.51) |
(0.26) |
(0.39) |
(0.36) |
(0.32) |
(0.3) |
(0.49) |
(0.39) |
(0.43) |
(0.3) |
(0.36) |
(0.41) |
(0.49) |
(0.39) |
(0.25) |
(0.36) |
(0.32) |
(0.37) |
(0.28) |
(0.26) |
(0.34) |
(0.57) |
(0.38) |
(0.36) |
(0.31) |
(0.43) |
(0.3) |
(0.34) |
(0.4) |
(0.55) |
(0.32) |
(0.33) |
(0.26) |
(0.4) |
(0.25) |
(0.31) |
(0.37) |
(0.39) |
(0.29) |
(0.34) |
(0.38) |
(0.53) |
(0.3) |
(0.39) |
(0.31) |
(0.34) |
(0.39) |
(0.36) |
(0.3) |
(0.47) |
(0.36) |
(0.39) |
(0.4) |
(0.39) |
(0.35) |
(0.37) |
(0.42) |
(0.27) |
(0.31) |
(0.35) |
(0.36) |
(0.39) |
(0.34) |
(0.35) |
(0.35) |
(0.26) |
(0.42) |
(0.33) |
(0.31) |
(0.3) |
(0.35) |
(0.29) |
(0.28) |
(0.32) |
(0.33) |
(0.36) |
(0.28) |
(0.32) |
(0.28) |
(0.31) |
(0.21) |
(0.45) |
(0.4) |
(0.29) |
(0.32) |
(0.43) |
(0.28) |
(0.35) |
(0.3) |
(0.26) |
(0.32) |
(0.39) |
(0.31) |
(0.43) |
(0.37) |
(0.36) |
(0.26) |
(0.24) |
(0.29) |
(0.38) |
(0.39) |
(0.36) |
(0.31) |
(0.35) |
(0.39) |
(0.3) |
(0.36) |
(0.35) |
(0.2) |
(0.27) |
(0.33) |
(0.29) |
(0.36) |
(0.37) |
(0.33) |
(0.36) |
(0.43) |
(0.32) |
(0.41) |
(0.41) |
(0.37) |
(0.4) |
(0.38) |
(0.44) |
(0.33) |
(0.31) |
(0.32) |
(0.3) |
(0.37) |
(0.27) |
(0.41) |
(0.28) |
(0.28) |
| 3 | (0.36) |
(0.28) |
(0.3) |
(0.25) |
(0.28) |
(0.32) |
(0.24) |
(0.25) |
(0.53) |
(0.29) |
(0.28) |
(0.28) |
(0.31) |
(0.4) |
(0.4) |
(0.35) |
(0.25) |
(0.38) |
(0.26) |
(0.32) |
(0.35) |
(0.31) |
(0.28) |
(0.46) |
(0.35) |
(0.42) |
(0.29) |
(0.36) |
(0.4) |
(0.42) |
(0.36) |
(0.24) |
(0.35) |
(0.31) |
(0.35) |
(0.28) |
(0.23) |
(0.27) |
(0.42) |
(0.36) |
(0.36) |
(0.3) |
(0.43) |
(0.3) |
(0.32) |
(0.39) |
(0.53) |
(0.28) |
(0.32) |
(0.25) |
(0.36) |
(0.25) |
(0.31) |
(0.34) |
(0.34) |
(0.28) |
(0.33) |
(0.35) |
(0.42) |
(0.28) |
(0.39) |
(0.3) |
(0.32) |
(0.39) |
(0.2) |
(0.29) |
(0.43) |
(0.34) |
(0.32) |
(0.38) |
(0.29) |
(0.32) |
(0.35) |
(0.3) |
(0.25) |
(0.31) |
(0.32) |
(0.35) |
(0.35) |
(0.26) |
(0.34) |
(0.34) |
(0.25) |
(0.36) |
(0.32) |
(0.28) |
(0.29) |
(0.35) |
(0.28) |
(0.28) |
(0.26) |
(0.3) |
(0.32) |
(0.28) |
(0.3) |
(0.26) |
(0.31) |
(0.2) |
(0.39) |
(0.39) |
(0.28) |
(0.29) |
(0.41) |
(0.25) |
(0.34) |
(0.3) |
(0.24) |
(0.3) |
(0.37) |
(0.3) |
(0.35) |
(0.31) |
(0.3) |
(0.21) |
(0.24) |
(0.27) |
(0.36) |
(0.36) |
(0.34) |
(0.31) |
(0.33) |
(0.38) |
(0.19) |
(0.34) |
(0.34) |
(0.19) |
(0.24) |
(0.32) |
(0.28) |
(0.36) |
(0.28) |
(0.31) |
(0.35) |
(0.41) |
(0.32) |
(0.25) |
(0.4) |
(0.31) |
(0.33) |
(0.3) |
(0.41) |
(0.3) |
(0.3) |
(0.29) |
(0.29) |
(0.33) |
(0.25) |
(0.37) |
(0.28) |
(0.27) |
| 4 | (0.36) |
(0.23) |
(0.3) |
(0.25) |
(0.26) |
(0.27) |
(0.23) |
(0.22) |
(0.43) |
(0.28) |
(0.24) |
(0.25) |
(0.31) |
(0.36) |
(0.36) |
(0.3) |
(0.23) |
(0.37) |
(0.26) |
(0.31) |
(0.32) |
(0.31) |
(0.26) |
(0.31) |
(0.29) |
(0.35) |
(0.26) |
(0.33) |
(0.36) |
(0.41) |
(0.34) |
(0.24) |
(0.31) |
(0.3) |
(0.34) |
(0.28) |
(0.23) |
(0.27) |
(0.31) |
(0.29) |
(0.3) |
(0.29) |
(0.38) |
(0.26) |
(0.3) |
(0.36) |
(0.49) |
(0.23) |
(0.3) |
(0.24) |
(0.35) |
(0.23) |
(0.28) |
(0.31) |
(0.3) |
(0.27) |
(0.28) |
(0.33) |
(0.41) |
(0.26) |
(0.35) |
(0.3) |
(0.31) |
(0.36) |
(0.2) |
(0.28) |
(0.41) |
(0.29) |
(0.32) |
(0.31) |
(0.29) |
(0.3) |
(0.29) |
(0.28) |
(0.23) |
(0.28) |
(0.29) |
(0.31) |
(0.32) |
(0.23) |
(0.31) |
(0.32) |
(0.23) |
(0.35) |
(0.32) |
(0.27) |
(0.26) |
(0.3) |
(0.27) |
(0.27) |
(0.25) |
(0.3) |
(0.32) |
(0.26) |
(0.3) |
(0.25) |
(0.3) |
(0.19) |
(0.27) |
(0.34) |
(0.25) |
(0.29) |
(0.41) |
(0.24) |
(0.34) |
(0.28) |
(0.18) |
(0.27) |
(0.36) |
(0.3) |
(0.31) |
(0.26) |
(0.28) |
(0.2) |
(0.23) |
(0.26) |
(0.32) |
(0.32) |
(0.34) |
(0.3) |
(0.27) |
(0.29) |
(0.18) |
(0.33) |
(0.31) |
(0.17) |
(0.2) |
(0.29) |
(0.28) |
(0.24) |
(0.23) |
(0.3) |
(0.32) |
(0.31) |
(0.29) |
(0.25) |
(0.39) |
(0.28) |
(0.29) |
(0.28) |
(0.38) |
(0.3) |
(0.28) |
(0.27) |
(0.28) |
(0.32) |
(0.24) |
(0.36) |
(0.26) |
(0.25) |
| 5 | (0.31) |
(0.22) |
(0.27) |
(0.25) |
(0.26) |
(0.26) |
(0.22) |
(0.22) |
(0.39) |
(0.25) |
(0.21) |
(0.24) |
(0.28) |
(0.33) |
(0.35) |
(0.28) |
(0.21) |
(0.34) |
(0.24) |
(0.29) |
(0.32) |
(0.29) |
(0.23) |
(0.3) |
(0.29) |
(0.32) |
(0.25) |
(0.31) |
(0.3) |
(0.4) |
(0.33) |
(0.22) |
(0.28) |
(0.3) |
(0.33) |
(0.25) |
(0.22) |
(0.27) |
(0.28) |
(0.28) |
(0.29) |
(0.27) |
(0.33) |
(0.24) |
(0.29) |
(0.36) |
(0.38) |
(0.23) |
(0.28) |
(0.24) |
(0.29) |
(0.22) |
(0.27) |
(0.28) |
(0.28) |
(0.26) |
(0.25) |
(0.33) |
(0.36) |
(0.25) |
(0.27) |
(0.24) |
(0.31) |
(0.35) |
(0.2) |
(0.28) |
(0.4) |
(0.27) |
(0.3) |
(0.31) |
(0.28) |
(0.26) |
(0.29) |
(0.27) |
(0.22) |
(0.25) |
(0.28) |
(0.3) |
(0.3) |
(0.21) |
(0.31) |
(0.23) |
(0.22) |
(0.29) |
(0.29) |
(0.24) |
(0.25) |
(0.3) |
(0.23) |
(0.27) |
(0.24) |
(0.29) |
(0.31) |
(0.26) |
(0.29) |
(0.25) |
(0.3) |
(0.18) |
(0.27) |
(0.32) |
(0.24) |
(0.27) |
(0.28) |
(0.24) |
(0.33) |
(0.26) |
(0.18) |
(0.27) |
(0.31) |
(0.22) |
(0.27) |
(0.26) |
(0.26) |
(0.2) |
(0.21) |
(0.25) |
(0.3) |
(0.28) |
(0.26) |
(0.3) |
(0.26) |
(0.28) |
(0.18) |
(0.3) |
(0.3) |
(0.15) |
(0.2) |
(0.28) |
(0.27) |
(0.23) |
(0.23) |
(0.29) |
(0.29) |
(0.29) |
(0.28) |
(0.24) |
(0.3) |
(0.26) |
(0.29) |
(0.28) |
(0.35) |
(0.28) |
(0.28) |
(0.26) |
(0.27) |
(0.32) |
(0.23) |
(0.32) |
(0.24) |
(0.24) |
▼LSIで得られたベクトルの類似度(ランク: 20)
| Ranking | Aatrox |
Ahri |
Akali |
Alistar |
Amumu |
Anivia |
Annie |
Aphelios |
Ashe |
AurelionSol |
Azir |
Bard |
Blitzcrank |
Brand |
Braum |
Caitlyn |
Camille |
Cassiopeia |
Chogath |
Corki |
Darius |
Diana |
Draven |
DrMundo |
Ekko |
Elise |
Evelynn |
Ezreal |
Fiddlesticks |
Fiora |
Fizz |
Galio |
Gangplank |
Garen |
Gnar |
Gragas |
Graves |
Hecarim |
Heimerdinger |
Illaoi |
Irelia |
Ivern |
Janna |
JarvanIV |
Jax |
Jayce |
Jhin |
Jinx |
Kaisa |
Kalista |
Karma |
Karthus |
Kassadin |
Katarina |
Kayle |
Kayn |
Kennen |
Khazix |
Kindred |
Kled |
KogMaw |
Leblanc |
LeeSin |
Leona |
Lissandra |
Lucian |
Lulu |
Lux |
Malphite |
Malzahar |
Maokai |
MasterYi |
MissFortune |
MonkeyKing |
Mordekaiser |
Morgana |
Nami |
Nasus |
Nautilus |
Neeko |
Nidalee |
Nocturne |
Nunu |
Olaf |
Orianna |
Ornn |
Pantheon |
Poppy |
Pyke |
Qiyana |
Quinn |
Rakan |
Rammus |
RekSai |
Renekton |
Rengar |
Riven |
Rumble |
Ryze |
Sejuani |
Senna |
Sett |
Shaco |
Shen |
Shyvana |
Singed |
Sion |
Sivir |
Skarner |
Sona |
Soraka |
Swain |
Sylas |
Syndra |
TahmKench |
Taliyah |
Talon |
Taric |
Teemo |
Thresh |
Tristana |
Trundle |
Tryndamere |
TwistedFate |
Twitch |
Udyr |
Urgot |
Varus |
Vayne |
Veigar |
Velkoz |
Vi |
Viktor |
Vladimir |
Volibear |
Warwick |
Xayah |
Xerath |
XinZhao |
Yasuo |
Yorick |
Yuumi |
Zac |
Zed |
Ziggs |
Zilean |
Zoe |
Zyra |
Rhaast |
ShadowAssassin |
| 1 | (0.8) |
(0.77) |
(0.73) |
(0.69) |
(0.69) |
(0.77) |
(0.64) |
(0.59) |
(0.95) |
(0.78) |
(0.71) |
(0.71) |
(0.77) |
(0.94) |
(0.82) |
(0.67) |
(0.81) |
(0.94) |
(0.73) |
(0.68) |
(0.8) |
(0.68) |
(0.71) |
(0.85) |
(0.81) |
(0.74) |
(0.77) |
(0.73) |
(0.73) |
(0.84) |
(0.73) |
(0.8) |
(0.72) |
(0.82) |
(0.8) |
(0.74) |
(0.76) |
(0.69) |
(0.86) |
(0.75) |
(0.73) |
(0.75) |
(0.9) |
(0.62) |
(0.79) |
(0.8) |
(0.95) |
(0.8) |
(0.75) |
(0.78) |
(0.88) |
(0.89) |
(0.78) |
(0.73) |
(0.67) |
(0.69) |
(0.62) |
(0.83) |
(0.93) |
(0.74) |
(0.89) |
(0.68) |
(0.74) |
(0.75) |
(0.62) |
(0.76) |
(0.9) |
(0.75) |
(0.81) |
(0.68) |
(0.7) |
(0.8) |
(0.75) |
(0.79) |
(0.81) |
(0.88) |
(0.93) |
(0.8) |
(0.74) |
(0.78) |
(0.68) |
(0.68) |
(0.6) |
(0.85) |
(0.78) |
(0.92) |
(0.8) |
(0.82) |
(0.69) |
(0.7) |
(0.83) |
(0.78) |
(0.86) |
(0.75) |
(0.82) |
(0.74) |
(0.76) |
(0.68) |
(0.78) |
(0.92) |
(0.78) |
(0.72) |
(0.84) |
(0.74) |
(0.77) |
(0.77) |
(0.61) |
(0.75) |
(0.76) |
(0.89) |
(0.85) |
(0.73) |
(0.81) |
(0.72) |
(0.67) |
(0.78) |
(0.7) |
(0.82) |
(0.84) |
(0.68) |
(0.83) |
(0.69) |
(0.67) |
(0.65) |
(0.8) |
(0.81) |
(0.72) |
(0.8) |
(0.75) |
(0.61) |
(0.75) |
(0.68) |
(0.76) |
(0.85) |
(0.81) |
(0.73) |
(0.86) |
(0.75) |
(0.75) |
(0.86) |
(0.86) |
(0.84) |
(0.67) |
(0.81) |
(0.76) |
(0.93) |
(0.7) |
(0.85) |
(0.8) |
(0.69) |
| 2 | (0.69) |
(0.69) |
(0.71) |
(0.66) |
(0.68) |
(0.67) |
(0.62) |
(0.59) |
(0.91) |
(0.75) |
(0.64) |
(0.65) |
(0.76) |
(0.8) |
(0.75) |
(0.58) |
(0.73) |
(0.84) |
(0.69) |
(0.68) |
(0.77) |
(0.68) |
(0.68) |
(0.85) |
(0.73) |
(0.7) |
(0.65) |
(0.68) |
(0.68) |
(0.79) |
(0.69) |
(0.67) |
(0.71) |
(0.8) |
(0.75) |
(0.62) |
(0.71) |
(0.67) |
(0.85) |
(0.72) |
(0.67) |
(0.75) |
(0.88) |
(0.62) |
(0.75) |
(0.75) |
(0.93) |
(0.74) |
(0.73) |
(0.71) |
(0.69) |
(0.72) |
(0.77) |
(0.64) |
(0.62) |
(0.66) |
(0.6) |
(0.75) |
(0.91) |
(0.73) |
(0.81) |
(0.68) |
(0.7) |
(0.72) |
(0.6) |
(0.69) |
(0.85) |
(0.71) |
(0.8) |
(0.64) |
(0.66) |
(0.69) |
(0.69) |
(0.72) |
(0.72) |
(0.7) |
(0.9) |
(0.8) |
(0.71) |
(0.63) |
(0.63) |
(0.61) |
(0.59) |
(0.8) |
(0.74) |
(0.86) |
(0.64) |
(0.78) |
(0.68) |
(0.69) |
(0.71) |
(0.77) |
(0.83) |
(0.74) |
(0.76) |
(0.68) |
(0.74) |
(0.67) |
(0.73) |
(0.83) |
(0.68) |
(0.71) |
(0.83) |
(0.61) |
(0.75) |
(0.75) |
(0.6) |
(0.67) |
(0.72) |
(0.88) |
(0.76) |
(0.6) |
(0.7) |
(0.61) |
(0.65) |
(0.74) |
(0.69) |
(0.7) |
(0.8) |
(0.66) |
(0.8) |
(0.67) |
(0.67) |
(0.64) |
(0.75) |
(0.79) |
(0.67) |
(0.72) |
(0.72) |
(0.6) |
(0.75) |
(0.67) |
(0.68) |
(0.8) |
(0.75) |
(0.69) |
(0.83) |
(0.72) |
(0.74) |
(0.82) |
(0.75) |
(0.81) |
(0.63) |
(0.62) |
(0.75) |
(0.85) |
(0.64) |
(0.73) |
(0.66) |
(0.59) |
| 3 | (0.67) |
(0.66) |
(0.71) |
(0.61) |
(0.66) |
(0.63) |
(0.6) |
(0.58) |
(0.78) |
(0.64) |
(0.63) |
(0.62) |
(0.69) |
(0.73) |
(0.73) |
(0.57) |
(0.64) |
(0.77) |
(0.64) |
(0.67) |
(0.72) |
(0.65) |
(0.63) |
(0.85) |
(0.7) |
(0.7) |
(0.6) |
(0.67) |
(0.64) |
(0.78) |
(0.69) |
(0.64) |
(0.69) |
(0.71) |
(0.72) |
(0.61) |
(0.65) |
(0.66) |
(0.7) |
(0.68) |
(0.61) |
(0.67) |
(0.85) |
(0.62) |
(0.68) |
(0.73) |
(0.83) |
(0.61) |
(0.7) |
(0.63) |
(0.69) |
(0.57) |
(0.6) |
(0.63) |
(0.6) |
(0.63) |
(0.58) |
(0.73) |
(0.82) |
(0.64) |
(0.69) |
(0.65) |
(0.7) |
(0.72) |
(0.59) |
(0.65) |
(0.85) |
(0.68) |
(0.75) |
(0.61) |
(0.64) |
(0.67) |
(0.65) |
(0.68) |
(0.62) |
(0.67) |
(0.9) |
(0.79) |
(0.71) |
(0.55) |
(0.62) |
(0.61) |
(0.54) |
(0.71) |
(0.72) |
(0.81) |
(0.57) |
(0.75) |
(0.67) |
(0.64) |
(0.63) |
(0.66) |
(0.82) |
(0.69) |
(0.75) |
(0.6) |
(0.72) |
(0.67) |
(0.72) |
(0.78) |
(0.65) |
(0.68) |
(0.78) |
(0.56) |
(0.72) |
(0.74) |
(0.6) |
(0.66) |
(0.65) |
(0.81) |
(0.75) |
(0.57) |
(0.68) |
(0.59) |
(0.65) |
(0.69) |
(0.67) |
(0.68) |
(0.75) |
(0.63) |
(0.75) |
(0.66) |
(0.53) |
(0.61) |
(0.69) |
(0.77) |
(0.67) |
(0.55) |
(0.69) |
(0.57) |
(0.75) |
(0.64) |
(0.67) |
(0.76) |
(0.75) |
(0.68) |
(0.72) |
(0.69) |
(0.73) |
(0.75) |
(0.74) |
(0.81) |
(0.62) |
(0.62) |
(0.75) |
(0.82) |
(0.62) |
(0.72) |
(0.64) |
(0.54) |
| 4 | (0.67) |
(0.64) |
(0.62) |
(0.58) |
(0.58) |
(0.59) |
(0.59) |
(0.57) |
(0.78) |
(0.63) |
(0.62) |
(0.61) |
(0.67) |
(0.71) |
(0.69) |
(0.56) |
(0.63) |
(0.77) |
(0.63) |
(0.63) |
(0.71) |
(0.65) |
(0.61) |
(0.56) |
(0.62) |
(0.62) |
(0.57) |
(0.65) |
(0.61) |
(0.78) |
(0.65) |
(0.63) |
(0.65) |
(0.62) |
(0.7) |
(0.61) |
(0.64) |
(0.66) |
(0.64) |
(0.6) |
(0.6) |
(0.65) |
(0.84) |
(0.62) |
(0.67) |
(0.69) |
(0.79) |
(0.59) |
(0.68) |
(0.62) |
(0.58) |
(0.55) |
(0.57) |
(0.62) |
(0.59) |
(0.63) |
(0.58) |
(0.68) |
(0.78) |
(0.62) |
(0.65) |
(0.65) |
(0.69) |
(0.7) |
(0.57) |
(0.61) |
(0.81) |
(0.68) |
(0.74) |
(0.54) |
(0.63) |
(0.65) |
(0.59) |
(0.67) |
(0.61) |
(0.6) |
(0.89) |
(0.77) |
(0.69) |
(0.55) |
(0.6) |
(0.6) |
(0.54) |
(0.66) |
(0.7) |
(0.75) |
(0.56) |
(0.74) |
(0.62) |
(0.59) |
(0.56) |
(0.64) |
(0.75) |
(0.69) |
(0.7) |
(0.57) |
(0.68) |
(0.64) |
(0.69) |
(0.73) |
(0.63) |
(0.68) |
(0.72) |
(0.54) |
(0.68) |
(0.73) |
(0.59) |
(0.61) |
(0.6) |
(0.79) |
(0.71) |
(0.52) |
(0.63) |
(0.59) |
(0.64) |
(0.68) |
(0.65) |
(0.67) |
(0.69) |
(0.62) |
(0.73) |
(0.61) |
(0.52) |
(0.6) |
(0.67) |
(0.69) |
(0.61) |
(0.54) |
(0.67) |
(0.55) |
(0.69) |
(0.61) |
(0.62) |
(0.59) |
(0.68) |
(0.64) |
(0.69) |
(0.63) |
(0.72) |
(0.75) |
(0.73) |
(0.8) |
(0.6) |
(0.6) |
(0.74) |
(0.8) |
(0.6) |
(0.6) |
(0.54) |
(0.53) |
| 5 | (0.66) |
(0.61) |
(0.62) |
(0.58) |
(0.57) |
(0.58) |
(0.57) |
(0.56) |
(0.75) |
(0.63) |
(0.61) |
(0.59) |
(0.66) |
(0.64) |
(0.68) |
(0.55) |
(0.61) |
(0.66) |
(0.62) |
(0.6) |
(0.68) |
(0.64) |
(0.61) |
(0.53) |
(0.58) |
(0.6) |
(0.54) |
(0.6) |
(0.54) |
(0.78) |
(0.65) |
(0.63) |
(0.59) |
(0.62) |
(0.69) |
(0.6) |
(0.58) |
(0.65) |
(0.6) |
(0.59) |
(0.59) |
(0.64) |
(0.82) |
(0.58) |
(0.64) |
(0.67) |
(0.75) |
(0.57) |
(0.64) |
(0.59) |
(0.56) |
(0.52) |
(0.52) |
(0.61) |
(0.57) |
(0.61) |
(0.56) |
(0.64) |
(0.72) |
(0.62) |
(0.6) |
(0.57) |
(0.66) |
(0.7) |
(0.56) |
(0.6) |
(0.81) |
(0.66) |
(0.73) |
(0.52) |
(0.6) |
(0.62) |
(0.56) |
(0.67) |
(0.6) |
(0.59) |
(0.81) |
(0.7) |
(0.67) |
(0.55) |
(0.59) |
(0.58) |
(0.53) |
(0.59) |
(0.68) |
(0.68) |
(0.53) |
(0.72) |
(0.62) |
(0.58) |
(0.54) |
(0.61) |
(0.73) |
(0.66) |
(0.65) |
(0.57) |
(0.68) |
(0.63) |
(0.65) |
(0.7) |
(0.63) |
(0.66) |
(0.69) |
(0.53) |
(0.65) |
(0.65) |
(0.58) |
(0.61) |
(0.6) |
(0.78) |
(0.63) |
(0.51) |
(0.61) |
(0.57) |
(0.56) |
(0.64) |
(0.64) |
(0.63) |
(0.68) |
(0.6) |
(0.65) |
(0.59) |
(0.52) |
(0.56) |
(0.63) |
(0.65) |
(0.6) |
(0.53) |
(0.66) |
(0.54) |
(0.69) |
(0.6) |
(0.61) |
(0.59) |
(0.64) |
(0.58) |
(0.67) |
(0.61) |
(0.68) |
(0.71) |
(0.65) |
(0.78) |
(0.59) |
(0.57) |
(0.72) |
(0.79) |
(0.58) |
(0.59) |
(0.52) |
(0.48) |
低ランク近似行列を使っているだけあって、LSIで得られたベクトルのほうが全体的に、高い類似度を得られていることがわかります。
分類
先ほどの類似度の表を見ていると、いくつかのグループに分かれていそうに見えたので、K近傍法を使って、分類してみました。
クラスタの数は、Riot Games APIでチャンピオンについているTagsの数と同じ6としています。
種類としては、Mage, Support, Fighter, Tank, Assassin, Marksmanの6つあり、これらに綺麗に分かれそうかなというかんじで決めました。これも詳しくは検討できていません。
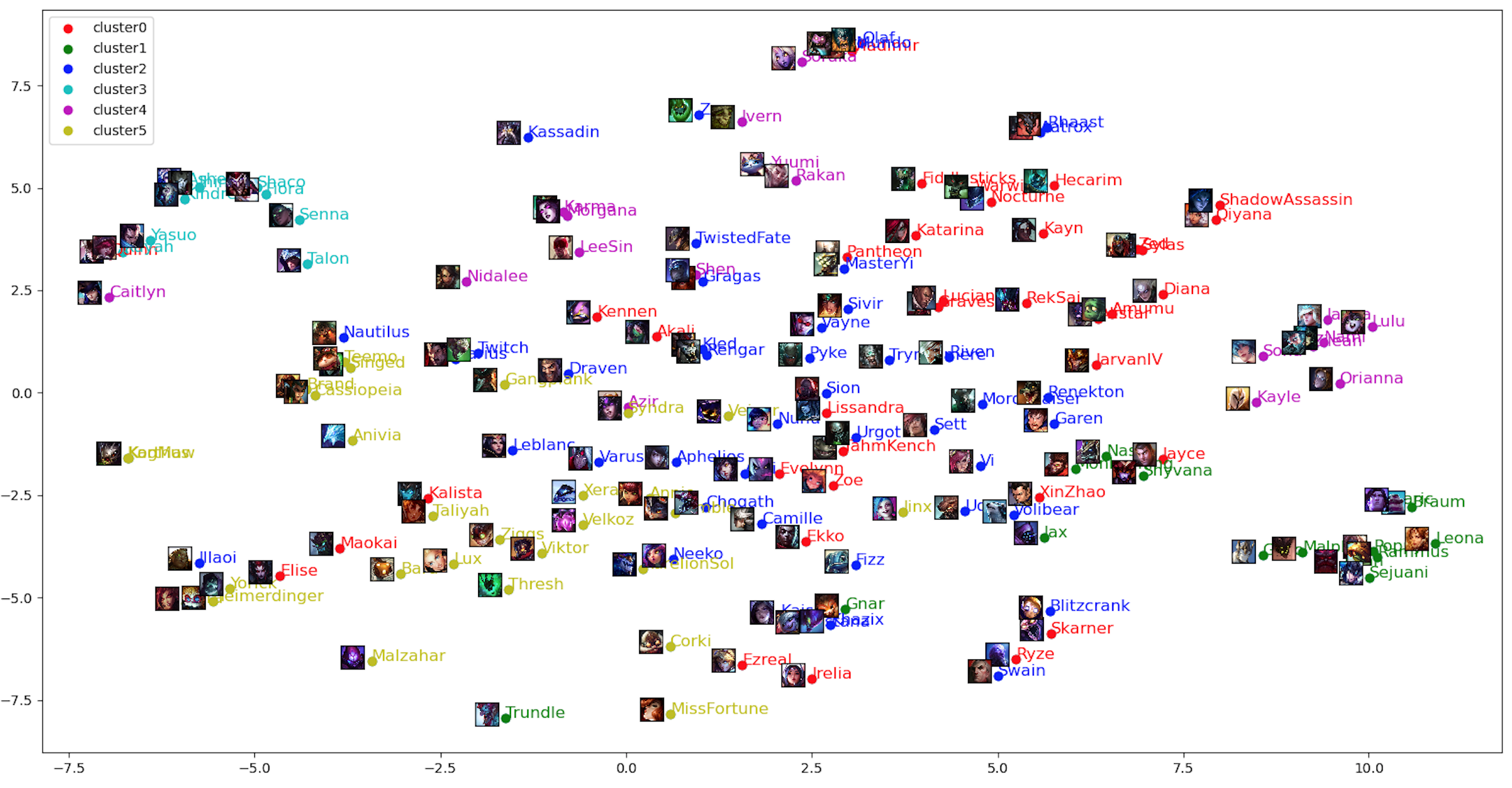
この結果を、t分布型確率的近傍埋め込み法 (t-SNE)で2次元に次元を削減したグラフとともに示しています。
t-SNEは高次元のものを可視化のために次元を削減する手法で、高次元での「近さ」を表現しているものだと考えてください。
以下に結果を示します。(上下の図でclusterの種類は別物で、色も対応していないことに注意してください。)
▼tfidfで得られたベクトルの分類とt-SNEの結果
▼LSIで得られたベクトルの分類とt-SNEの結果
※KogMawの後ろにはKarthusが隠れています。
トピック
考察できそうなトピックは得られませんでした。詳しくは後述します。
考察と今後の課題
類似度
まずは、ランキングをみると、低ランク近似を行なっていてもランキングが変わらないチャンピオンや(例: 、)、大きく変わるチャンピオン(例: 、)がいることが見受けられます。
特にアニーに関しては、アイバーンのRの性能(ペット要素)が酷似していることから、tfidfでは類似度が高く評価されていると考えられます。
しかし、LSIでの結果では、他のペット要素(タレット、子グモ、苗木)を持っていて、スタンやスネアを持っているチャンピオンが上位に来ていることがわかります。
これは潜在意味を考慮されたため、他のペット要素、足止めスキルを評価された結果だと考えられます。
ほとんどのチャンピオンにおいて、ランキングに登場するチャンピオンが大きく変化せず、1から3チャンピオンほど変わっていることを見ると、LSIの結果は、tfidfでの結果を残しつつ、潜在意味を考慮した結果を反映できているとみることができます。
個人的な総評としては、おおむね良い類似度が得られているように思えます。
ただし、中には本当に似ているのか？と疑う結果もあります。
具体的には、アジールがユーミやアイバーンといったようなサポートチャンピオンと類似度が高い点です。
これは、アジールの
Eが味方の兵士を味方扱いしており、味方に飛びつきながらシールドを得る点がサポートチャンピオンと似ているとされていると考えられます。
このような細かい点は考慮できていないため、何かしらの対策を考えるかアジールをサポートチャンピオンと考えることで解決できます。
次に、1つのスキルの効果を持っていることにより、類似度が高くなってしまっている組み合わせがあることについて述べます。
具体的には、アッシュ、ジン、キンドレッドのようにクリティカルを保証しているスキルを持っており、それによって、クリティカルダメージが増減する効果も持っているものがあります。
クリティカルの保証とダメージ増減は、別のスキルの効果として考えているおり、クリティカルの保証を持っていると、他のスキルも高い確率で持っているため、類似度は高くなってしまいます。
他にもソラカ、ブラッドミア、ムンドのように、自身の体力を使ってスキルを使う代わりに、スキルに回復効果を持っているものも該当します。
このように、あるスキルを持っていることが、他のスキルを持っていることに影響を与える組は1つの効果として考えたほうが良い結果を得られるような気がしています。
これに該当するのは、今のところ見つけられているのは、体力をコストとして使うスキルとクリティカルの保証の2つです。
これに関しては、人間の理解が必要になるので、人手で行う必要があると思っています。
最後に、場面によって、類似度に採用するスキルの効果を取捨選択したほうがいいように思います。
というのも、今回はWikiに存在する項目ならすべて考慮しているため、私たちが思っている類似度に強く関係しているものと関係していないものがあります。
強く関係していないものの例として、アニビアのWとエズリアルのWはダメージを与えてもいないにも関わらず戦闘状態を解除するというような効果があります。
これを持っているのは上記2体を含めて6体となっており、tfidfを考慮すると、類似度が高くなってしまいます。
しかし、この効果がスタンやブリンクといった効果と同等に私たちが扱っているかどうかは考える余地はあります。
ただ、戦闘状態は関係していなさそうだから、という理由で除くわけにもいかないので、場面によって取捨選択をする必要があると思っています。
具体的には、視界を取る場面において、視界を取るスキルをどれくらい持っているかや戦闘においてどれだけ味方、敵に関係するスキルを持っているかという場合わけが必要だと思います。
これにより、強く関係していないものを除くことができるため、より人間の理解に近い類似度を求めることができると考えられます。
分類
次に分類した結果について。
tfidfとLSIで、近さが異なるチャンピオンの組み合わせは見受けられませんでした。
近似というだけあって、近さが変わっていないことがわかります。
LSIのクラスタをみると、cluster1, cluster4, cluster5 は近くにまとまっているものがあり、Tank, Support, Mageを意味していそうだと考えられます。
ただ他のTagとclusterを対応づけるのは難しそうです。
たとえば、cluster3は近くにまとまっていますが、類似度の考察でも述べたようにクリティカル関係で集まっています。その中には、アサシン、マークスマン、ファイターと呼ばれているチャンピオンを含むため、どのTagが当てはまるかを考えることは難しいです。
その他のclusterに関しても、様々なTagを持つチャンピオンが存在するため、どのTagが対応しているかを考えるのは難しそうです。
ただ、Marksmanの大きな特徴としては、射程が長いことがあり、今回はそれを考慮していません。
それを考えると、当初の目的だった近接チャンピオンと遠隔チャンピオンの類似度を求められることになり、広い視野を得られているとも考えることができます。
また、K近傍法は1つのクラスタに分類しますが、混合ガウスモデルを使って、2つ以上の要素を持つことを考慮すると、綺麗な分かれ方をするかもしれません。
今回混合ガウスモデルを使ってないのは、それをどう図示しようかが決まらなかったので、行なっていません。
そもそも、クラスタの数が6個以上存在する可能性もあります。分類を行うためには、さらに検討することが多そうです。
トピック
今回は、結果に載せられるようなトピックを得られませんでした。
ただ、トピックが得られなかったわけではありません。
トピックは得られたのですが、そのトピックの内容が負の値を含むものであったため、考察が難しいという結果になりました。
LSIはランク削減として、素晴らしい手法なのですが、トピックの負の値に意味を持たないという欠点があります。
意味を持たないのはトピックのみで、それを使った行列には、低いランクで近似した行列という意味を持つので考察は可能です。
トピック毎の正の値を上から見ていき、考察できるかと思いましたが、負の値ありきでトピックが調整されているとすると、正の値の意味にも影響を与えるため、考察できませんでした。
これは、潜在意味解析の中でも明らかになっていることで、この問題について解決する方法も提案されています。
それは、潜在的ディリクレ配分法(Latent Dirichlet Allocation, LDA)を使うことです。
今回は、その元となった手法であるLSIでやってみたらどのようになるのかを見てみたかったため、LSIを使いました。
ただ、トピック間の関係をみるためには、LDAを使う必要があると思っています。
LDAを説明するためには、結構な量があるのと、説明できるほど理解できていないので、今後の課題にしています。
おわりに
Wikiの情報にもとづき、スキルの効果でチャンピオンを表現し、tfidfとLSIで新たなベクトルを取得し、そのベクトルの類似度を求めました。
LSIのほうが類似度は高くなっていますが、tfidfも決して悪い方法ではありません。
類似度こそ低いですが、特定のチャンピオンを示したいときには、tfidfのほうが有利です。
たとえば、スリープを持っているチャンピオンという指定をしたい場合は、tfidfで得られた行列を使うことが適切です。
場面によっての使い分けが必要です。
今回得られたベクトルは完璧なわけではなく、さらに良いものにするための今後の課題としては、
- LDAを使ったトピック間の関係の考察
- 場面によるスキルの取捨選択
- あるスキルを持っていることが、他のスキルを持っていることに影響を与える組の削除
があります。
どれから着手するか、それとも一旦先に進んでしまうか、迷いどころですが、結果を見ながら選んでいきたいと思います。
間違いや不明点などありましたらお気軽に聞いていただけると幸いです。
最後まで読んでいただき、ありがとうございました。
